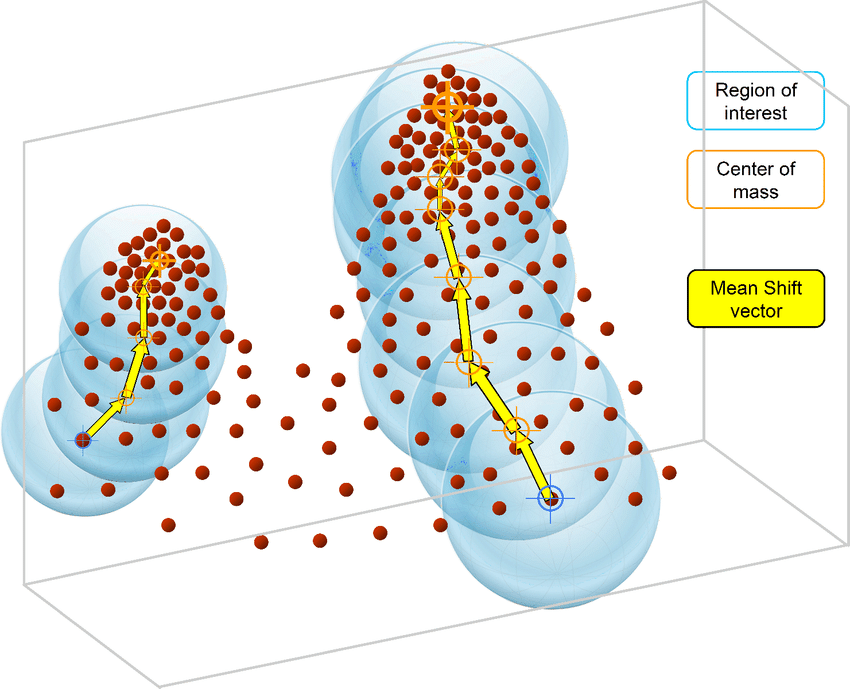
Mean Shift is an unsupervised machine learning algorithm. It is a hierarchical data clustering algorithm that finds the number of clusters a feature space should be divided into, as well as the location of the clusters and their centers. It works by grouping data points according to a “bandwidth”, a distance around data points, and converging the clusters’ centers towards the densest regions of data.
How to program the K-Means clustering algorithm
K-Means is a popular unsupervised machine learning algorithm for data clustering. A typical start for flat clustering, the K-Means algorithm works by defining a number K of clusters to be extracted by the algorithm. With this K number given, the algorithm will then find the best “centroids” to cluster the data around.
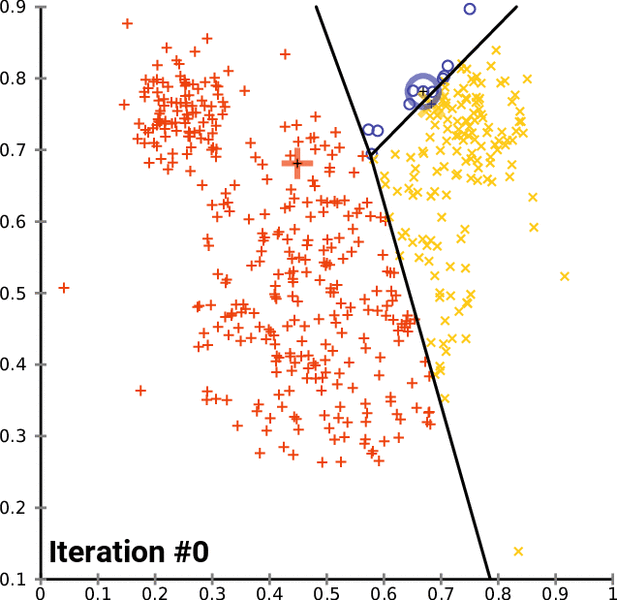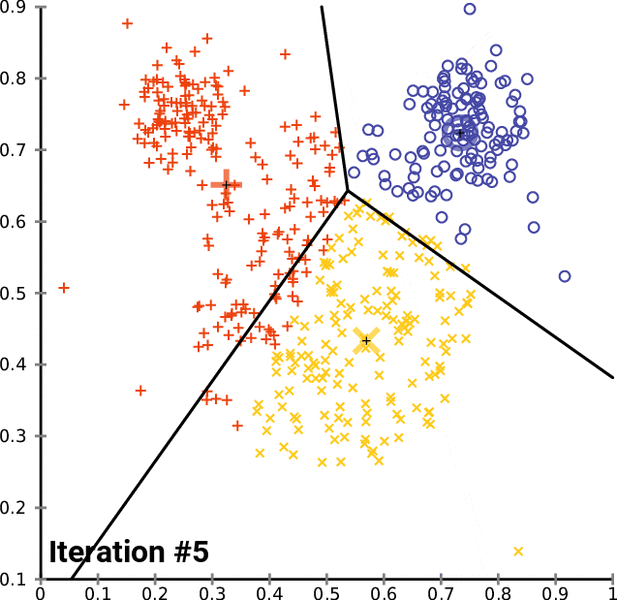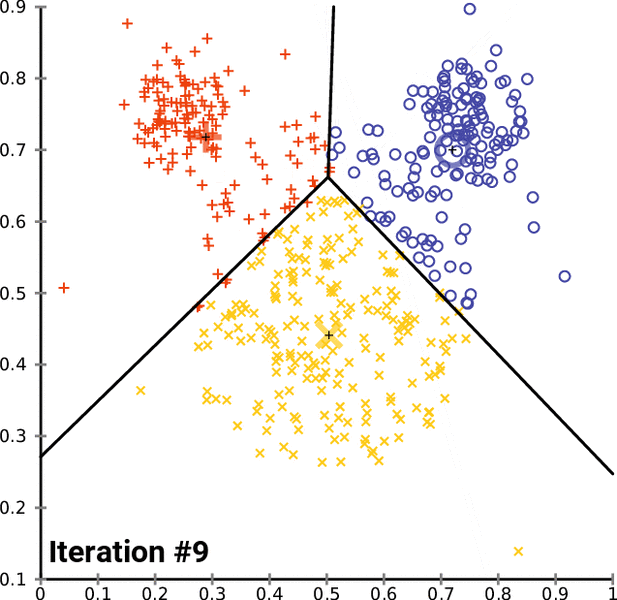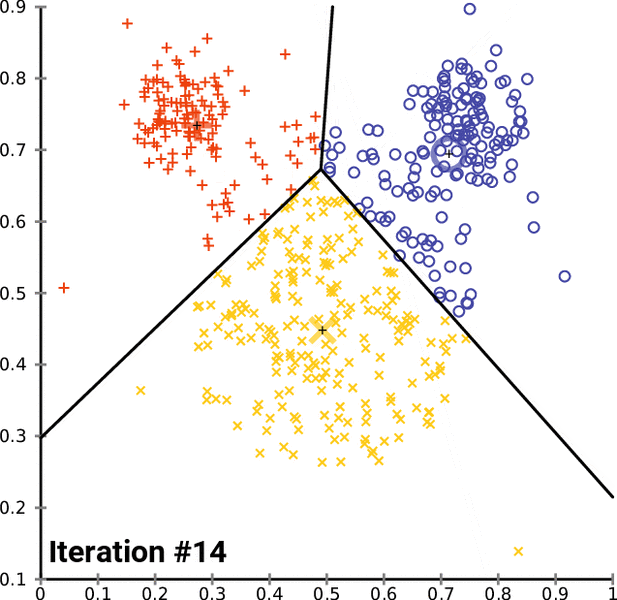Continue reading “How to program the K-Means clustering algorithm”
How to program the Support Vector Machines algorithm
Support Vector Machine is one of the most commonly used supervised machine learning algorithms for data classification. A binary classifier, the support vector machine algorithm works in vector space to sort data points by finding the best hyperplane separating them into two groups. Thanks to its reliance upon vectors, it finds frontiers between groups of data points even in nonlinear patterns and features spaces of high dimensions.
Continue reading “How to program the Support Vector Machines algorithm”
How to program the K Nearest Neighbors algorithm
K Nearest Neighbors is a popular classification algorithm for supervised machine learning. It permits to divide data points into groups, defining a model that will then be able to classify an unknown data point in one group or another. The K parameter, defined during programming, allows the algorithm to classify unknown data points by examining the K closest known data points.
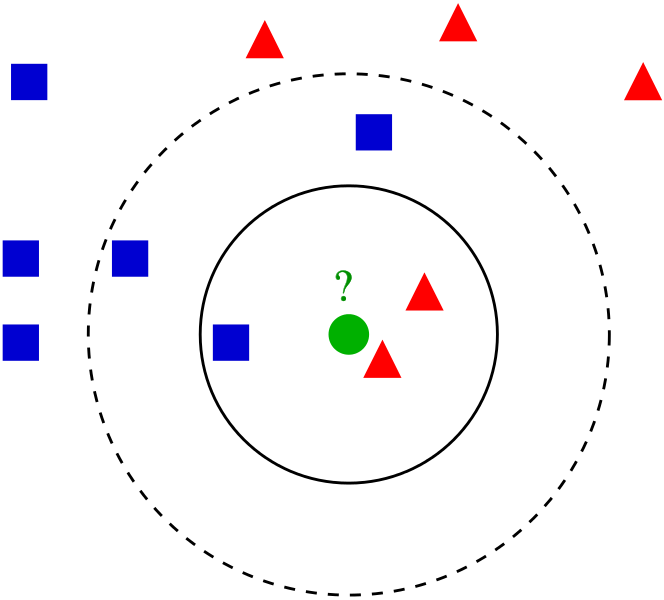Continue reading “How to program the K Nearest Neighbors algorithm”
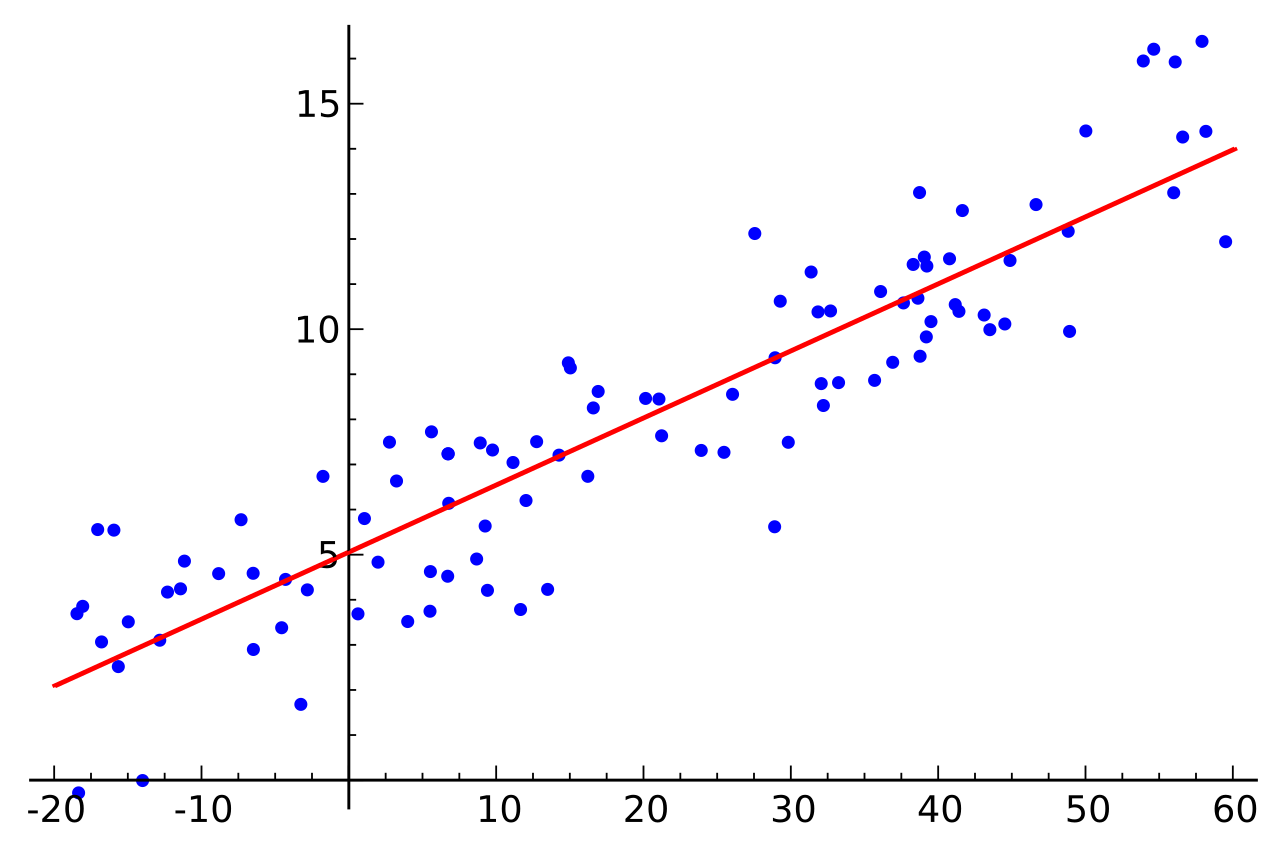
How to program a Linear Regression
One of the simplest supervised machine learning tools used in data science, linear regression permits to find the best-fitting line that correlates data points in a two-dimensional space. Defining this line then enables the prediction of where other data points could be located in the space, if they have the same characteristics as the original data set or if they stand out of it.
